README.md

1411. Number of Ways to Paint N × 3 Grid

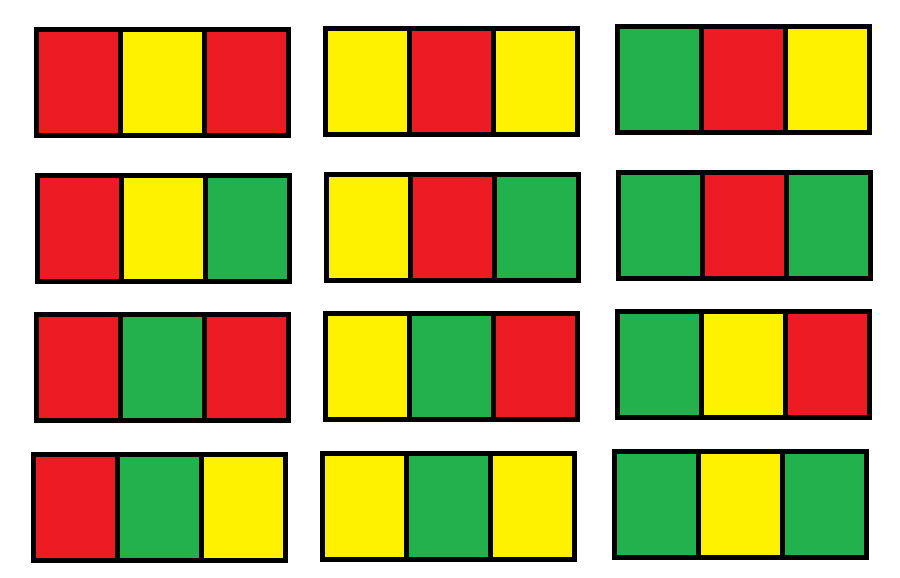
You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colors: Red, Yellow, or Green while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).

Given n the number of rows of the grid, return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 109 + 7.

Example 1:

Input: n = 1 Output: 12 Explanation: There are 12 possible way to paint the grid as shown. 

Example 2:

Input: n = 5000 Output: 30228214 

Constraints:

• n == grid.length
• 1 <= n <= 5000

Solutions (Rust)

1. Solution

implSolution{pubfnnum_of_ways(n:i32) -> i32{letmut x = 6;letmut y = 6;for _ in1..n { x = (x + y) % 1_000_000_007*2 % 1_000_000_007; y = (x + y) % 1_000_000_007;}(x + y) % 1_000_000_007}}